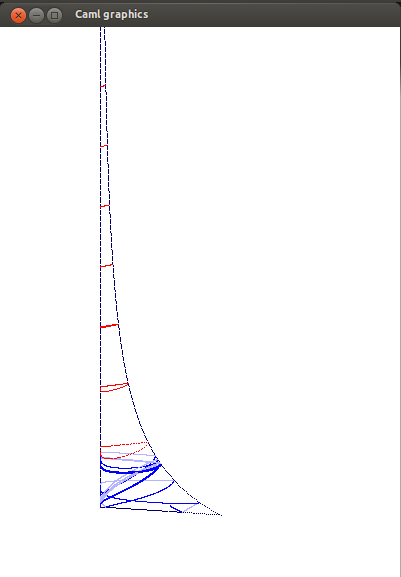
Geodesic flow on a homogeneous space

In blue, some geodesic rays on the moduli space $ \mathrm{SL}(2,\mathbb{Z}) \backslash \mathrm{SL}(2,\mathbb{R}) / \mathrm{SO}(2) $ (non isometrically) embedded into $\mathbb{R}^3$. Below the two singular points (order $2$ on the left, order $3$ on the right); in red horocycles. On the left: rational geodesic, diving right into the cusp. In the middle: convergence towards a periodic geodesic (here the second shortest). On the right: unbounded height. The third case happens almost surely in the sense of the Liouville measure. Moreover, if we put $h$ the height and $H_t = \sup_{s < t} h(s)$ then $\limsup \log H_t / \log t$ is almost surely $1$ (Sullivan 1982), and $H_t /t$ converges in law to a Fréchet's law (Guivarc'h, Le Page 2013).